Constitutive modeling of some 2D crystals: Graphene, hexagonal BN, MoS2, WSe2 and NbSe2

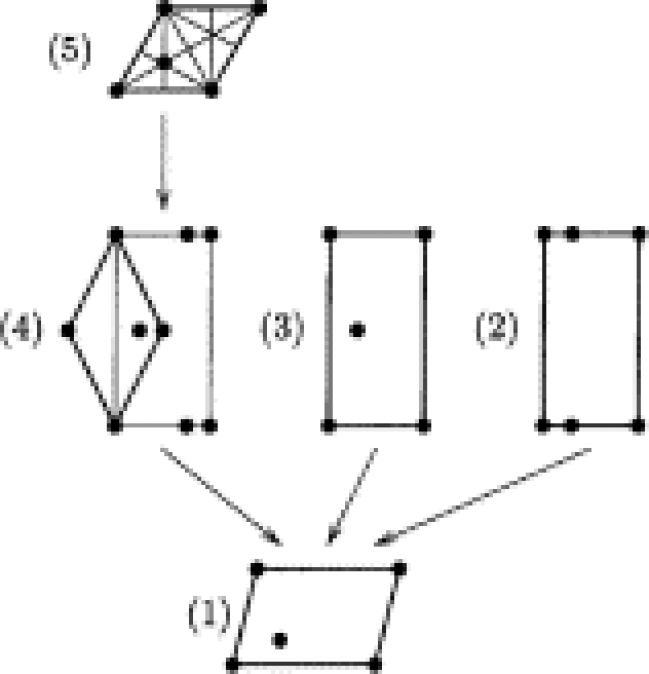
We lay down a nonlinear elastic constitutive framework for the modeling of some 2D crystals of current interest. The 2D crystals we treat are graphene, hexagonal boron nitride and some metal dichalcogenides: molybdenium disulfide (MoS₂), tungsten selenium (WSe₂), and niobium diselenide (NbSe₂). We first find their arithmetic symmetries by using the theory of monoatomic and diatomic 2-nets. Then, by confinement to weak transformation neighborhoods and by applying the Cauchy–Born rule we are able to use the symmetries continuum mechanics utilizes: geometric symmetries.

We give the complete and irreducible representation for energies depending on an in-plane measure, the curvature tensor and the shift vector. This is done for the symmetry hierarchies that describe how symmetry changes at the continuum level: C_6ν→C_2ν→C₁C6ν→C2ν→C1 for monoatomic 2-nets, and C_6ν→C_1ν→C₁C6ν→C1ν→C1 for diatomic two nets. We stress that we do not take into account how energy behaves at the transition regime. Having these energies at hand we are able to evaluate stresses and couple stresses for each symmetry regime. These quantities participate to the field equations: the momentum equation, the moment of momentum equation and the equation ruling the shift vector.

By making specific assumption for the loading histories that correspond to in-plane biaxial tension/compression as well as in-plane simple shear, we obtain necessary expressions for the shift vector components in order all field equations to be satisfied. When the algebraic equations ruling the shift vector render infinite solutions, we use the Cauchy–Kowalevski theorem-when it applies-for the momentum equation viewed as a quasilinear system in order to single out the unique solution.